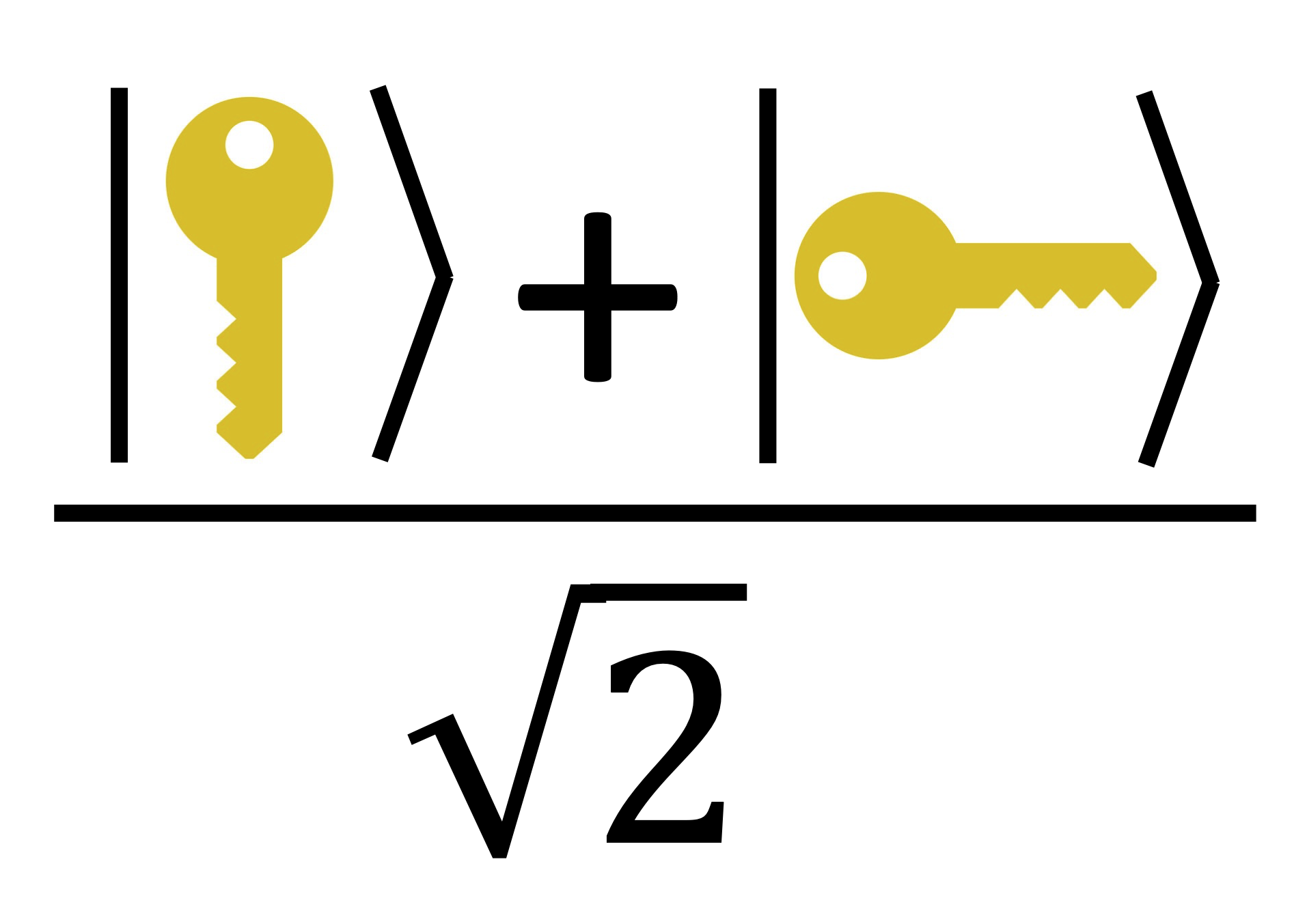
MIT 6.S895 (Spring 2024)
Quantum Cryptography

Announcements

[2/23] Problem Set 1 is posted here, due midnight on Friday March 8th. Submit your solutions on Canvas.
[2/13] Tuesday's class is canceled as MIT is closed for the snowstorm!
[2/6] Problem Set 0 is posted here. This is only so you can calibrate your understanding of the quantum basics. You do not need to turn it in.
Lecture videos are available at this page. You need to have MIT certificates to access the videos.

Course Description

This course is an introduction to the many ways quantum computing and cryptography intersect. Topics will include uniquely quantum cryptographic primitives such as quantum key distribution and quantum money, post-quantum cryptography (classical cryptography that is secure against quantum attackers), the use of cryptography in verifying quantum devices, as well as unclonable cryptography. Some familiarity with both quantum computing and cryptography is assumed.

The audience is graduate students interested in quantum computing, cryptography, or more broadly the theory of computing. Students are expected to have some familiarity with the basic notions of quantum computing and cryptography, and to be mathematically mature (comfortable with writing proofs, and with linear algebra and basic notions in group theory and number theory).

Prerequisites: Students are expected to be familiar with the basics of quantum information and computation (at the level of 6.6410, Quantum Computation, or 6.6420, Quantum Information Science) and the basics of cryptography (at the level of 6.5620 Foundations of Cryptography) or obtain the permission of instructors.

Course Information

INSTRUCTORS	Anand Natarajan Email: anandn at mit dot edu Vinod Vaikuntanathan Email: vinodv at mit dot edu
LOCATION AND TIME	Tuesday and Thursday 11:00-12:30pm in 45-102 (in the new Schwarzman College of Computing building).
TAs	Tina Zhang Email: tinaz at mit dot edu Office hours: TBD. Location: TBD.
RESOURCES	The main references will be the course materials including lecture notes, slides and/or videos. We will also post relevant papers after every lecture. Here are a few supplementary references for the entire course material. Lecture notes John Preskill's Caltech lecture notes on quantum computation Ronald de Wolf's CWI lecture notes Ryan O'Donnell's CMU lecture notes on quantum information and computation Andrew Childs' Maryland lecture notes on quantum algorithms Ma and Vazirani's Berkeley course on quantum cryptography Henry Yuen's Columbia course on quantum complexity and cryptography. Khurana's UIUC course on quantum cryptography Textbooks Nielsen and Chuang's classic book Watrous' book on quantum information (online version) Scott Aaronson's textbook (online version) Vidick and Wehner's book on quantum cryptography
PIAZZA	We will use Piazza for class communication. Please ask your questions there, so that other students can see the questions and answers.
ASSIGNMENTS AND GRADING	Grades will be determined based on 2 problem sets (20% each) and a final project, including a project presentation and a writeup (60%). The final projects can be done in groups of at most two.
COLLABORATION POLICY	Collaboration is permitted and encouraged in small groups of at most three students. You are free to collaborate in discussing answers, but you must write up solutions on your own, and must specify in your submission the names of any collaborators. Do not copy any text from your collaborators; the writeup must be entirely your work. Do not write down solutions on a board and copy it verbatim into Latex; again, the writeup must be entirely your own words and your own work and should demonstrate clear understanding of the solution. Additionally, you may make use of published material, provided that you acknowledge all sources used.

Schedule (tentative and subject to change)

Lecture	Topic
Lecture 1 (Tue Feb 6)	Quantum bootcamp + the Wiesner money scheme [Lecture Notes]
Lecture 2 (Thu Feb 8)	Attacks on Wiesner: cloning, Lutomirski's attack, Quantum Zeno Effect and the Elitzur-Vaidman bomb [Lecture Notes] References: Stephen Wiesner's paper A Brief History of Quantum Cryptography by Gilles Brassard Lutomirski's paper Nagaj, Sattath, Brodutch and Unruh's paper Aaronson's stackexchange post Molina, Vidick and Watrous' paper
Lecture 3 (Tue Feb 13)	Canceled due to "snowstorm"
Lecture 4 (Thu Feb 15)	BB84 key exchange and security sketch References: Security of Quantum Key Distribution by Renato Renner
Tue Feb 20 Monday Schedule of Classes
Lecture 5 (Thu Feb 22)	Symmetric subspace and de Finetti theorem References: The Church of the Symmetric Subspace by Aram Harrow A simple proof of Renner's exponential de Finetti theorem by Thomas Vidick and Henry Yuen Unknown Quantum States: The Quantum de Finetti Representation by Carlton M. Caves, Christopher A. Fuchs, and Ruediger Schack
Lecture 6 (Tue Feb 27)	BB84 Security Analysis Concluded: Information Reconciliation, Privacy Amplification, and Uncertainty References: The uncertainty principle: variations on a theme by Avi Wigderson and Yuval Wigderson Entropic Uncertainty Relations and their Applications by Patrick J. Coles, Mario Berta, Marco Tomamichel, and Stephanie Wehner Chapter 8 of Vidick and Wehner A Monogamy-of-Entanglement Game With Applications to Device-Independent Quantum Cryptography by Marco Tomamichel, Serge Fehr, Jędrzej Kaniewski, and Stephanie Wehner Sampling in a Quantum Population, and Applications by Niek J. Bouman and Serge Fehr. This paper gives a different (simpler?) analysis of BB84.
Lecture 7 (Thu Feb 29)	Beyond BB84: Impossibility of Quantum Bit Commitment/ Uhlmann's theorem References: Unconditionally secure quantum bit commitment is impossible by Dominic Mayers Is Quantum Bit Commitment Really Possible? by Hoi-Kwong Lo and H. F. Chau A brief review on the impossibility of quantum bit commitment by Gilles Brassard, Claude Crépeau, Dominic Mayers, and Louis Salvail In class we followed Nielsen and Chuang's proof of Uhlmann's theorem, but an alternate presentation is in Chapter 3 of Watrous
Lecture 8 (Tue Mar 5)	Post-quantum Security 1: Pseudo-random Functions, Collapse-Binding [Lecture Notes] References: How to Construct Quantum Random Functions by Mark Zhandry Computationally Binding Quantum Commitments by Dominique Unruh Quantum Attacks on Classical Proof Systems: The Hardness of Quantum Rewinding by Ambainis, Rossmanis and Unruh On the Necessity of Collapsing for Post-Quantum and Quantum Commitments by Marcell dell'Agnol and Nicholas Spooner.
Lecture 9 (Thu Mar 7)	Post-quantum Security 2: Collapse-Binding (Contd.) and Its Applications References: New Constructions of Collapsing Hashes by Zhandry
Lecture 10 (Tue Mar 12)	Jordan Lemma, Watrous Rewinding and Zero Knowledge against Quantum Attacks References: Zero-knowledge against Quantum Attacks by Watrous
Lecture 11 (Thu Mar 14)	Rewinding and Zero-Knowledge (continued) Guest Lecturer: Alex Lombardi
Lecture 12 (Tue Mar 19)	Commitments and Oblivious Transfer from One-way Functions References: One-way Functions Imply Secure Computation in a Quantum World by Bartusek, Coladangelo, Khurana and Ma. Oblivious Transfer is in MiniQCrypt by Grilo, Lin, Song and Vaikuntanathan. Improving the Security of Quantum Protocols via Commit-and-Open by Damgard, Fehr, Lunemann, Salvail and Schaffner. Advanced Reading: A New Framework for Quantum Oblivious Transfer by Agarwal, Bartusek, Khurana and Kumar.
Lecture 13 (Thu Mar 21)	Pseudorandom Quantum States (PRS): definition and construction Guest Lecturer: Alex Poremba [Lecture Notes] References: Pseudorandom Quantum States by Ji, Liu and Song (Pseudo) Random Quantum States with Binary Phase by Brakerski and Shmueli Pseudorandom (Function-Like) Quantum State Generators by Ananth, Gulati, Qian and Yuen Introduction to Haar Measure Tools in Quantum Information: A Beginner's Tutorial by Mele Quantum Pseudorandomness and Classical Complexity by Kretschmer
Tue Mar 26 Spring Break
Thu Mar 28 Spring Break
Lecture 14 (Tue Apr 2)	Commitments from PRS, and oracle PRSs from weak assumptions Guest Lecturer: Luowen Qian [Lecture Notes] References: On the computational hardness needed for quantum cryptography by Brakerski, Canetti and Qian. Quantum Cryptography in Algorithmica by Kretschmer, Qian, Sinha and Tal. A one-query lower bound for unitary synthesis and breaking quantum cryptography by Lombardi, Ma and Wright. Pseudorandom unitaries with non-adaptive security by Metger, Poremba, Sinha and Yuen.
Lecture 15 (Thu Apr 4)	Lattices, Gaussians and Shor Factoring [Lecture Notes] References: Lecture Notes on Shor's Algorithm by Vazirani. Lattice Lecture Notes by Vaikuntanathan. Creating superpositions that correspond to efficiently integrable probability distributions by Grover and Rudolph.
Lecture 16 (Tue Apr 9)	Regev's Algorithm for Factoring. Guest Lecturer: Seyoon Ragavan References: An Efficient Quantum Factoring Algorithm by Regev. Space-Efficient and Noise-Robust Quantum Factoring by Ragavan and Vaikuntanathan. Extending Regev’s factoring algorithm to compute discrete logarithms by Ekerä and Gartner.
Lecture 17 (Thu Apr 11)	Regev's worst-case to average-case reduction References: Lattice Lecture Notes by Vaikuntanathan.
Lecture 18 (Tue Apr 16)	Yamakawa-Zhandry Proof of Quantumness. References: Verifiable Quantum Advantage without Structure by Yamakawa and Zhandry.
Lecture 19 (Thu Apr 18)	Trapdoor Claw-free Functions and the BCMVV Proof of Quantumness References: A Cryptographic Test of Quantumness and Certifiable Randomness from a Single Quantum Device by Brakerski, Christiano, Mahadev, Vazirani and Vidick. Classically-Verifiable Quantum Advantage from a Computational Bell Test by Kahanamoku-Meyer, Choi, Vazirani and Yao.
Lecture 20 (Tue Apr 23)	Quantum FHE and the CHSH Protocol References: Classical Verification of Quantum Computations by Mahadev. Classical Homomorphic Encryption for Quantum Circuits by Mahadev. Quantum Advantage from Any Non-Local Game by Kalai, Lombardi, Vaikuntanathan and Yang.
Lecture 21 (Thu Apr 25)	Proofs of Quantumness: Extracting and measuring a qubit References: Classical Verification of Quantum Computations by Mahadev. Classical Homomorphic Encryption for Quantum Circuits by Mahadev. Quantum Advantage from Any Non-Local Game by Kalai, Lombardi, Vaikuntanathan and Yang. Interactions with Quantum Devices: Lecture Notes by Thomas Vidick.
Lecture 22 (Tue Apr 30)	Testing multiqubit measurements: Pauli braiding + Gowers-Hatami References: Bounding the Quantum Value of Compiled Nonlocal Games: From CHSH to BQP Verification by Natarajan and Zhang.
Lecture 23 (Thu May 2)	Delegation and Remote State Preparation Guest Lecturer: Andru Gheorghiu References: Verification of quantum computation: An overview of existing approaches by Gheorghiu, Kapourniotis and Kashefi. Universal blind quantum computation by Broadbent, Fitzsimmons and Kashefi. Computationally-secure and composable remote state preparation by Gheorghiu and Vidick. Quantum cryptography with classical communication: parallel remote state preparation for copy-protection, verification, and more by Gheorghiu, Metger and Poremba.
Lecture 24 (Tue May 7)	Uncloneable Cryptography Guest Lecturer: Jiahui Liu References: Quantum Copy Protection and Quantum Money by Aaronson. Quantum Money from Hidden Subspaces by Aaronson and Christiano. Zhandry's course notes.
Lecture 25 (Thu May 9)	Student Presentations
Lecture 26 (Tue May 14)	Student Presentations

Resources (Quantum Information and Computation)

MIT 8.370 Quantum Computation Lecture notes.
MIT 8.S372/18.S996 Quantum Information Science 3. Lecture notes are available here.

Resources (Cryptography)

MIT 6.5620
Pass and Shelat's book